4 Greatest contributions of Srinivasa Ramanujan to mathematics:

Introduction:

“An equation means nothings to me unless it express a thought of GOD ”

                                                                               –Srinivasa Ramanujan

Srinivasa Ramanujan is one of the  greatest mathematician of all the time. It is impossible to cover all the contributions of Srinivasa Ramanujan to mathematics in this post. In this article, we highlight 4 greatest contributions of Srinivasa Ramanujan to mathematics.

4 greatest contributions of Srinivasa Ramanujan to mathematics:

1.  Infinite series for pi:

1.1 The number Pi: 

Pi is a mathematical constant which was first calculated by  Archimedes. He found its value to be 3.14159265358979… . In Mathematical language pi is defined to be the ratio between circumference of a circle and its diameter. In the history of mathematics, it has been always a challenge for mathematicians to calculate the correct approximation of pi.

1.2 Contributions of Srinivasa Ramanujan to calculate the value of pi:

   In the early age, Srinivasa Ramanujan had remarkable talent for mathematics. Though he had many problems in his early life but his interest towards mathematics remained unflinching. He slowly became popular for his extraordinary talent for mathematics despite lack of a university education. He wrote letters mentioning his results to many prominent mathematicians of that time trying to interest them in his results. His letters were ignored at first until the potentiality of his results were recognized by G.H. Hardy.

                      In the letter to Hardy, Ramanujan mentioned many infinite series, the famous one was the following series for pi:

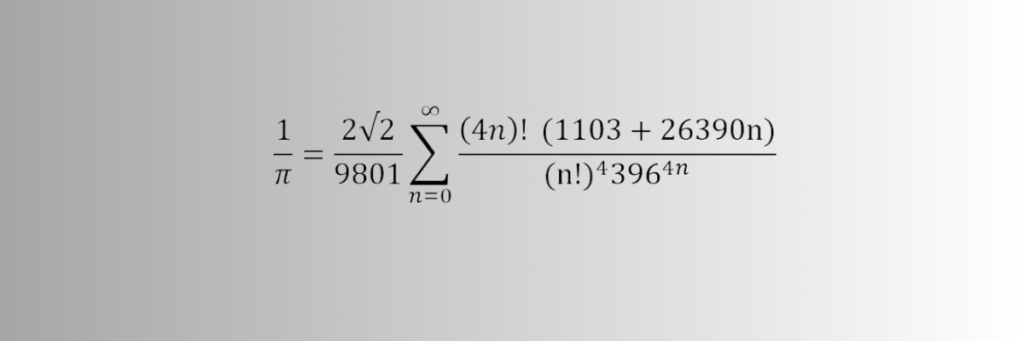
Putting n=0, the above expression gives the value pi which is correct up to six decimal place. Although there is no apparent explanation for how he arrived at the values in his method, this formula is absolute accurate for determining the value of π.

2. Partition function: 

2.1Partition of a integer:

In simple language, partition of an integer is the number of ways the integer can be expressed as sum of positive integers. For example, consider n=5. Then n=5 can be expressed as a sum of positive numbers in following ways:

                                                            5=5

                                                              =4+1

                                                              =3+2

                                                              =3+1+1

                                                              =2+1+1+1

                                                            =2+2+1

                                                            =1+1+1+1+1

The values of P(n) are 1,2,3.5,7,11,… for n=1,2,3,4,5,6… . As the value of n increase, the value of p(n) increase exponentially. For instance, the value of P(10) is 47 while the value of P(100) is 190569292. Instead of calculating the value of P(n), many mathematicians tried to formulate this partition function P(n). Srinivasa Ramanujan was one of them.

2.2 Contribution of Srinivasa Ramanujan to the partition function:

It is very difficult to calculate partition of a large positive number. The contribution of Srinivasa Ramanujan to calculate the value of partition of large number is very significant. Ramanujan, in collaboration with G. H. Hardy developed a formula to find the value of partition of large number. His formula is as follows:

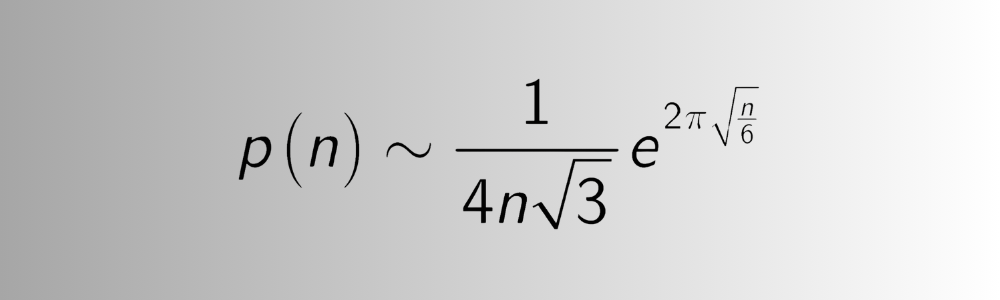
The above formula doesn’t provide the exact value but a very close approximation for large value of n.

Ramanujan also developed various properties related to the partition function. Some of them are  as below:

This partition function has many application in number theory, q-series and modular forms. 

3. A function in Srinivasa Ramanujan’s  dream:

In the last letter of Srinivasa Ramanujan to Hardy, Ramanujan mention functions that come to him in his dream. He also mentioned that these functions were revealed to him by the goddess Namagiri. Since Ramanujan died after few days, these functions remained unproven. Finally after 90 years, a group of mathematician was able prove it. Those functions in Ramanujan’s dreams are known as Mock Theta Functions.

4. The smallest number 1729…:

The significance of the number 1729 was recognized by Srinivasa Ramanujan during his conversation with G.H. Hardy. When Hardy came to meet Ramanujan in hospital, Hardy mentioned that the taxi number in which he came was a ‘’dull”. Then Ramanujan replied that 1729 is not a dull number, it is the smallest number which can be expressed as sum of two cube in two different ways.

The two mathematical expressions of the number 1729 are as follows:

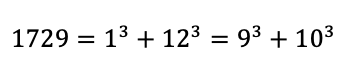
Conclusion:

Contributions of Srinivasa Ramanujan is very significant for his original and unique approach. His contributions have great impact on mathematics. It is a matter of curiosity, how with little formal education Srinivasa Ramanujan was able to construct those functions.India honour the contributions of Srinivasa Ramanujan by celebrating National Mathematics Day on 22nd December every year. 

If you like my posts, kindly share your comments. To read more blogs, click here.